Самое актуальное и обсуждаемое
Популярное
Полезные советы

Важно знать!
3д рисунки: топ-150 фото лучших способов и техник. поэтапный мастер-класс рисования для начинающих своими руками
Как создать трехмерный рисунок на бумаге
Характеристиками простого листа бумаги являются только длина и ширина. Для того чтобы создавать необычные рисунки, обладающие глубиной и объемом, необходимо разобраться...
Читать далее
15 лучших бетономешалок
12 лучших шведских стенок
7 способов экономно отопить дом электричеством
7 крутых постеров для интерьера, которые сможет нарисовать даже новичок
5 лучших энергосберегающих обогревателей для дома
9 лучших термопотов для дома и офиса
15 примеров золотого сечения в архитектуре
12 лучших газовых обогревателей для дачи на баллонном газе: рейтинг приборов и советы покупателям
10 соток это сколько метров в длину и ширину
Рекомендуем
Лучшее

Важно знать!
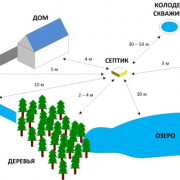
5 лучших сифонов для газирования воды
5 O!range
В сифоне O!range можно готовить любые газированные напитки – с фруктами, вареньем, сиропами, другими добавками. Изготовлен он достаточно качественно, а стоит недорого. По форме и принципу...
Читать далее
10 лучших столиков для ноутбука
10 лучших биметаллических радиаторов
31 фото бра в спальне над кроватью: приглушенный свет всегда актуален
48 фото идей того, как украсить магазин к новому году 2020 своими руками
4 подходящих материала для отделки и дизайна фасада частного дома
100+ фото плитки для ванной комнаты: лучшие дизайн проекты
9 разновидностей уличных печей для дачи и загородного дома + 50 фото и видео
10 лучших фабрик мягкой мебели в россии
5 лучших обогревателей для дачи
Новое
Обсуждаемое

Важно знать!
5 отличных вариантов шпаклевки для стен под обои с нюансами выбора и другими полезными советами: 50 фото и 2 видео
Важность выравнивания
Это удивительно, но многие люди порой искренне задают следующий 2 вопроса: «а зачем выравнивать стены под обои ?» и «а нужно ли грунтовать стены перед поклейкой обоев...
Читать далее
10 лучших раскладушек для сна
7 лучших оверлоков janome
4 способа расширить балкон в многоквартирном доме и при этом не нарушить закон
3 способа подключения греющего кабеля к сети при обогреве водопровода
10 лучших фирм теплиц из поликарбоната
8 способов прочистки труб от засоров
12 лучших болгарок (ушм)
4 бюджетных варианта как можно спрятать трубы в туалете
9 красивых и дешевых ножей в cs:go, с которыми не стыдно бегать
Популярное
Актуальное

Важно знать!
12 лучших токовых клещей
Режимы измерений
Применяют 2 метода определения силы тока:
прямое;
непрямое (индуктивное) измерение.
Первый способ производится при подсоединении амперметра к разрыву электрической цепи. Электроток...
Читать далее
11 лучших моющих пылесосов 2021
12 лучших акриловых ванн по отзывам специалистов
10 лучших материалов для облицовки фасада
12 лучших точилок для ножей
90+ идей как оформить дом к новому году 2021: ярко, стильно и креативно!
12 лучших растущих стульев для ребенка
20+ советов, как обустроить комнату для детей всех возрастов
4 супер-способа преображения стула и табуретки своими руками
3д панели для стен: самые интересные и новые идеи
Обновления
 Статьи
Эффективная скупка лома кабеля: Устойчивое строительство с вторичными ресурсами.
Статьи
Эффективная скупка лома кабеля: Устойчивое строительство с вторичными ресурсами.
В современном обществе, где устойчивость и корпоративная ответственность становятся важной составляющей...
 15 лучших обогревателей для дачи
15 лучших обогревателей для дачи
Принцип работы
Электрические обогреватели делятся на три категории по принципу работы:
за счет тепловой...
 11 лучших недорогих пылесосов
11 лучших недорогих пылесосов
Лучшие циклонные пылесосы со стандартными насадками
Нижеприведённые варианты рассчитаны на людей со...
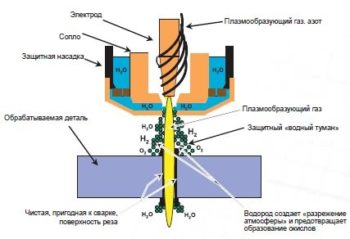 10 лучших плазморезов
10 лучших плазморезов
Преимущества метода плазменной резки
Плюсы этих устройств нужно хорошо знать, равно как и минусы, без...
 9 лучших вентиляторов в ванную комнату
9 лучших вентиляторов в ванную комнату
Виды приборов вентилирования для помещений
В санузлах используются два типа устройств – это изделия...
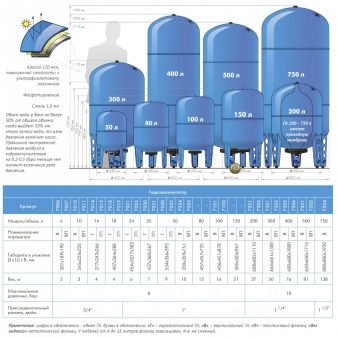 8931 500 03 90 8960 290 23 01как отрегулировать давление в гидроаккумуляторе
8931 500 03 90 8960 290 23 01как отрегулировать давление в гидроаккумуляторе
Преимущества от циркуляционного насоса
Включение в состав отопительной системы такого прибора имеет...
 10 советов по выбору столешницы для кухни
10 советов по выбору столешницы для кухни
5 важных советов
1. Столешница должна повторять цвет хотя бы одного элемента кухни
В идеале – двух элементов....
 3 главных этапа: как сделать душевую кабину в ванной комнате без поддона?
3 главных этапа: как сделать душевую кабину в ванной комнате без поддона?
Дверь или ограждение выбрать
Дверь предпочтительнее: полная изоляция кабинки, брызги воды не вылетают...
 2 дюйма
2 дюйма
Лучшие смартфоны на 4 дюйма с хорошей камерой
Хорошая камера – обязательное требование многих покупателей...
 100 см2 в м2
100 см2 в м2
Способ № 2
Вторым методом расчета удобно пользоваться в случаях, когда определяется количество рулонов...
 10 советов, как выбрать газовую колонку (газовый водонагреватель) для квартиры
10 советов, как выбрать газовую колонку (газовый водонагреватель) для квартиры
Газовая аппаратура должна быть безопасной для потребителей
Электронный цифровой дисплей газовой колонки
Как...
 13 лучших машинок для стрижки волос
13 лучших машинок для стрижки волос
Виды машинок для стрижки
Для начала нужно понять, какой тип подобного приспособления будет лучшим вариантом...